There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u).
There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected).
The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example 1:

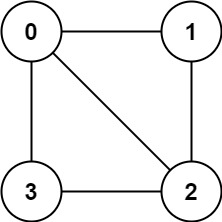
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

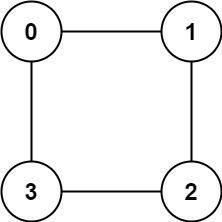
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.

Solution

Time complexity : O(N+E) (N : # nodes, E : # edges)
Space complexity : O(N)

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        const int n = graph.size();
        vector<int> color(n, -1);
        
        for (int i=0; i<n; ++i) {
            if (color[i] != -1)
                continue;
            stack<int> stk;
            stk.push(i);
            while (!stk.empty()) {
                int node = stk.top(); stk.pop();
                if (color[node] == -1) color[node] = 0;
                for (int neigh: graph[node]) {
                    if (color[neigh] == -1) {
                        stk.push(neigh);
                        color[neigh] = color[node] ^ 1;
                    } else if (color[node] == color[neigh])
                        return false;
                }
            }
        }
        
        return true;
    }
};

遍歷過所有 node ，且用 BFS 的方式檢查上色狀況。用 color 陣列記錄各個 node 被標記的顏色，-1 代表尚未標記，0 、 1 分別代表兩種不同顏色。