In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

  • Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
  • C_1 is at location (0, 0) (ie. has value grid[0][0])
  • C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
  • If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

Example 1:

Input: [[0,1],[1,0]]
Output: 2

Example 2:

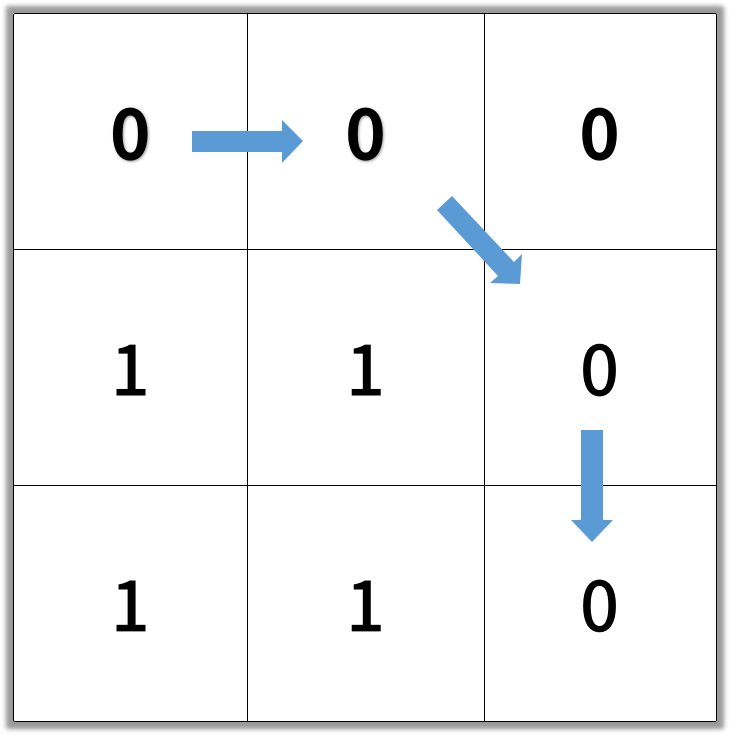
Input: [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Note:

  1. 1 <= grid.length == grid[0].length <= 100
  2. grid[r][c] is 0 or 1

Solution

BFS

Time complexity : O(rc)
Space complexity : O(1)

class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        const int rows = grid.size(), cols = grid[0].size();
        if (grid[0][0] != 0 || grid[rows-1][cols-1] != 0) return -1;
        vector<pair<int, int>> q;
        
        q.push_back({0, 0});
        int step = 0;
        
        while (!q.empty() && grid[rows-1][cols-1] <= 0) {
            ++step;
            
            // mark
            for (auto xy: q) {
                grid[xy.second][xy.first] = step;
            }
            
            // get next breadth
            vector<pair<int, int>> next_q;
            for (auto xy: q) {
                for (int dx = -1; dx <= 1; ++dx) {
                    for (int dy = -1; dy <= 1; ++dy) {
                        int x = xy.first+dx, y = xy.second+dy;
                        if (x<0 || cols<=x || y<0 || rows<=y)
                            continue;
                        if (grid[y][x] == 0) {
                            next_q.push_back({x, y});
                            grid[y][x] = -1;
                        }
                    }
                }
            }
            q = next_q;
        }
        return grid[rows-1][cols-1] == 0 ? -1 : grid[rows-1][cols-1];
    }
};

用 BFS 的方式，從左上走到右下。

每走一步 step 就加 1，並在腳下那塊記錄目前的 step。
再根據目前這一步走了哪些塊，尋找下一步要往哪走，往 0 的方向走，並標記 -1 ，代表該塊已記錄到下一步中。