Inorder Successor in BST

Given the root of a binary search tree and a node p in it, return the in-order successor of that node in the BST. If the given node has no in-order successor in the tree, return null.

The successor of a node p is the node with the smallest key greater than p.val.

Example 1:

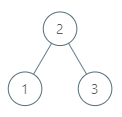
Input: root = [2,1,3], p = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both p and the return value is of TreeNode type.

Example 2:

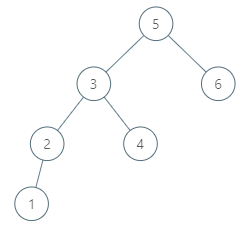
Input: root = [5,3,6,2,4,null,null,1], p = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• -10^5 <= Node.val <= 10^5
• All Nodes will have unique values.

---

Solution

Inorder traversal (iterative)

Time complexity : O(n)
Space complexity : O(n)

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        stack<TreeNode*> stk;
        TreeNode* curr = root;
        bool is_p = false;
        while (curr || !stk.empty()) {
            while (curr) {
                stk.push(curr);
                curr = curr->left;
            }
            curr = stk.top(); stk.pop();
            if (is_p) return curr;
            if (curr == p) is_p = true;
            curr = curr->right;
        }
        return nullptr;
    }
};

Inorder Traversal (recursive)

Time complexity : O(n)
Space complexity : O(n)

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        ans = nullptr;
        inorder(root, p);
        return ans;
    }
private:
    TreeNode *prev, *ans;
    void inorder(TreeNode* node, TreeNode* p) {
        if (!node) return;
        inorder(node->left, p);
        if (prev == p) ans = node;
        prev = node;
        inorder(node->right, p);
    }
};

BST Traversal (iterative)

Time complexity : O(n)
Space complexity : O(1)

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode* ans = nullptr;
        while (root) {
            if (root->val <= p->val)
                root = root->right;
            else {
                ans = root;
                root = root->left;
            }
        }
        return ans;
    }
};

BST Traversal (recursive)

Time complexity : O(n)
Space complexity : O(n)

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if (!root) return nullptr;
        if (root->val <= p->val)
            return inorderSuccessor(root->right, p);
        else {
            TreeNode *left_res = inorderSuccessor(root->left, p);
            return left_res ? left_res : root;
        }
    }
};