[LeetCode December Challange] Day 3 - Increasing Order Search Tree

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

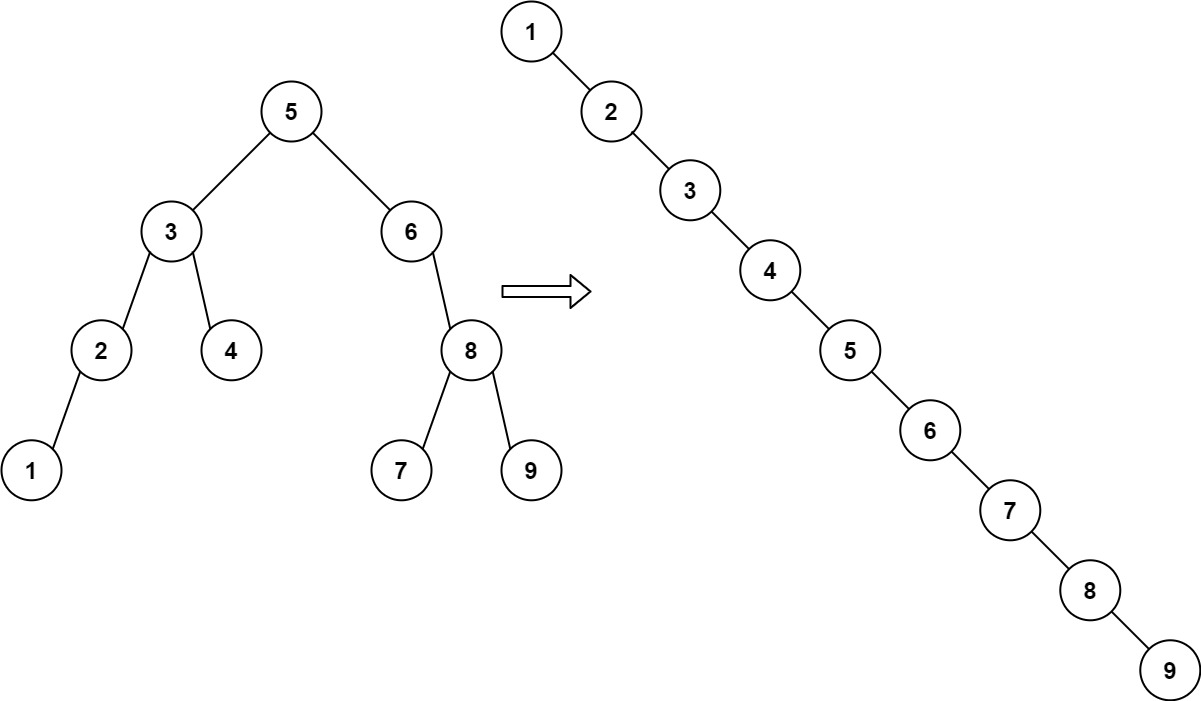
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

---

Solution

Time complexity : O(n)
Space complexity : O(h)

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode() : val(0), left(nullptr), right(nullptr) {}
*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
    TreeNode* increasingBST(TreeNode* root) {
        TreeNode dummy_head = TreeNode(0);
        cur = &dummy_head;
        inorder(root);
        return dummy_head.right;
    }

    void inorder(TreeNode* node) {
        if (!node) return;
        inorder(node->left);
        node->left = nullptr;
        cur->right = node;
        cur = node;
        inorder(node->right);
    }
private:
    TreeNode* cur;
};

創一個新的 dummy head ，因在 BST 上 inorder traverse 後的結果會是由小到大的結果，故以 inorder 的處理順序，依序把左子樹拿掉，連到 dummy head 那邊，更新目前尾巴的位置，即可。