Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Notice that you should not modify the linked list.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

Example 1:

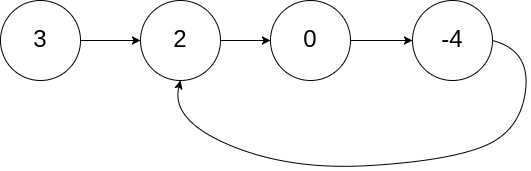
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

  • The number of the nodes in the list is in the range [0, 10^4].
  • -10^5 <= Node.val <= 10^5
  • pos is -1 or a valid index in the linked-list.

Solution

Time complexity : O(n)
Space complexity : O(1)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (!head) return nullptr;
        ListNode *fast = head, *slow = head;
        bool is_cyclic = false;
        while (fast->next && fast->next->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                is_cyclic = true;
                break;
            }
        }
        if (!is_cyclic) return nullptr;
        
        ListNode *slow2 = head;
        while (slow != slow2) {
            slow = slow->next;
            slow2 = slow2->next;
        }
        
        return slow;
    }
};

用的是Floyd’s Tortoise and Hare演算法。
分兩階段，第一階段找出是否是cycle及相遇的點，第二階段找出cycle的入口。

第一階段的做法，使用快慢指標，快的走兩步，慢的走一步，若有cycle，則快慢指標會走到一起。
記錄走到一起時，慢指標的位置，第二階段要用。

整二階段的做法，使用雙慢指標，一個從之前慢指標的位置開始走，另一個從頭開始走，相遇在一起的點，即是cycle的入口。