[LeetCode July Challange]Day1-Arranging Coins

You have a total of n coins that you want to form in a staircase shape, where every k-th row must have exactly k coins.

Given n, find the total number of full staircase rows that can be formed.

n is a non-negative integer and fits within the range of a 32-bit signed integer.

example 1

n = 5

The coins can form the following rows:  
 
¤  
¤ ¤  
¤ ¤  
  
Because the 3rd row is incomplete, we return 2.  

example 2

n = 8  

The coins can form the following rows:  
¤  
¤ ¤  
¤ ¤ ¤  
¤ ¤  

Because the 4th row is incomplete, we return 3.  

---

solution

time complexity : O(1)
space complexity : O(1)

class Solution {
public:
    int arrangeCoins(int n) {
        return (-1 + sqrt(8*static_cast<long>(n) + 1)) / 2;
    }
};

此題探討的是三角形數，第n個三角形數所需的coin數量為n(n+1)/2。
(2個相同的三角形數可組成一矩形)
例：第6個三角形數所需coin數量為6(6+1)/2=21

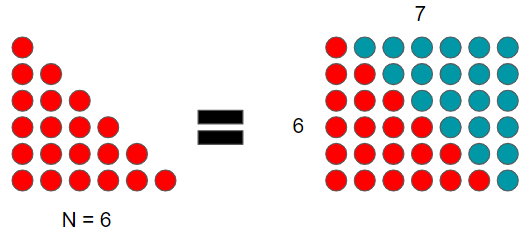
可利用一元二次方程式推導出若使用n個硬幣，
則可以堆出第(-1+sqrt(8*n + 1))/2個三角形數(取整數部份)。