Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0). Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Notice that you may not slant the container.

Example 1:

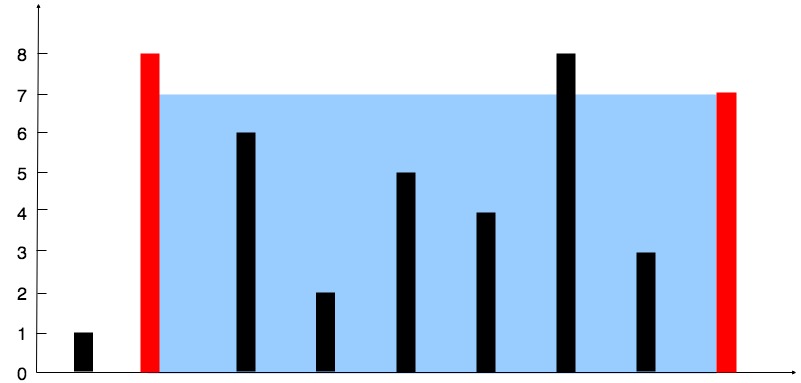
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

Example 3:

Input: height = [4,3,2,1,4]
Output: 16

Example 4:

Input: height = [1,2,1]
Output: 2

Constraints:

n == height.length
2 <= n <= 3 * 10^4
0 <= height[i] <= 3 * 10^4

Solution

Time complexity : O(n)
Space complexity : O(1)

class Solution {
public:
    int maxArea(vector<int>& height) {
        const int n = height.size();
        int ans = INT_MIN;
        int l = 0, r = n - 1;
        while (l < r) {
            int h = min(height[l], height[r]);
            ans = max(ans, h*(r-l));
            if (height[l] < height[r])
                ++l;
            else
                --r;
        }
        return ans;
    }
};

2 Pointers，Greedy，左右往中間跑，優先移動較短的，因較短的有較大的機會下一根比較長，而使 area 變大。