Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

  • The left subtree of a node contains only nodes with keys less than the node’s key.
  • The right subtree of a node contains only nodes with keys greater than the node’s key.
  • Both the left and right subtrees must also be binary search trees.

Note: This question is the same as 1038:

Example 1:

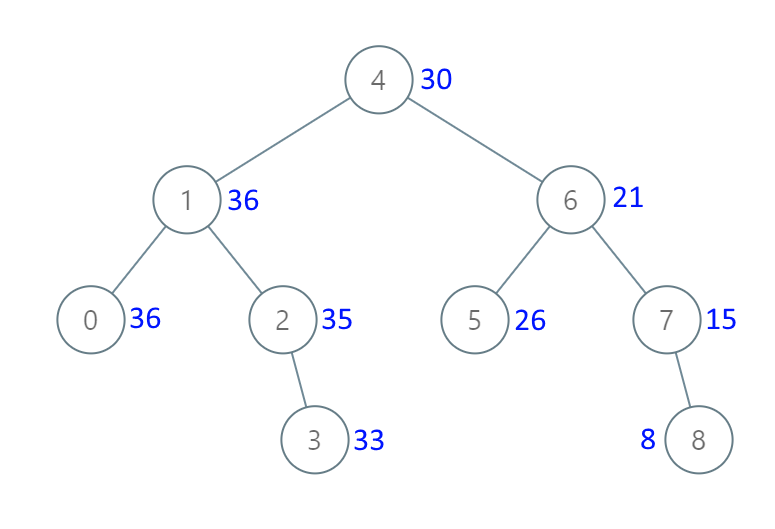
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Example 3:

Input: root = [1,0,2]
Output: [3,3,2]

Example 4:

Input: root = [3,2,4,1]
Output: [7,9,4,10]

Constraints:

  • The number of nodes in the tree is in the range [0, 10^4].
  • -10^4 <= Node.val <= 10^4
  • All the values in the tree are unique.
  • root is guaranteed to be a valid binary search tree.

Solution

Time complexity : O(n)
Space complexity : O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        dfs(root, 0);
        return root;
    }
private:
    int dfs(TreeNode* node, int acc) {
        if (node == nullptr) return acc;
        acc = dfs(node->right, acc);
        node->val += acc;
        acc = dfs(node->left, node->val);
        return acc;
    }
};

用 dfs 右中左的方式去遍歷整棵樹，以一個 node 的觀點來看：

  1. 將目前 acc 值往右子樹傳，並更新 acc 值。
  2. 此時 acc 為比此 node 還要大的值的總和，更新此 node 值。
  3. 將目前 acc 值(即更新後的此 node 值)往左子樹傳，並更新 acc 值。
  4. 回傳 acc 值給 parent node。