Given the head of a linked list, return the list after sorting it in ascending order.

Follow up: Can you sort the linked list in O(n logn) time and O(1) memory (i.e. constant space)?

Example 1:

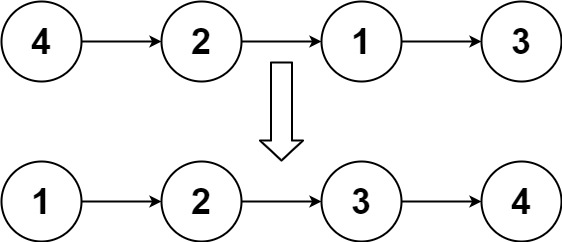
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]

Example 3:

Input: head = []
Output: []

Constraints:

The number of nodes in the list is in the range [0, 5 * 104].
-105 <= Node.val <= 105

Solution

Top-Down link-list merge sort.

Time complexity : O(n log(n))
Space complexity : O(log(n))

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (!head || !head->next) return head;
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }
        ListNode *second_head = slow->next;
        slow->next = nullptr;
        return merge(sortList(head), sortList(second_head));
    }
private:
    ListNode* merge(ListNode* l1, ListNode* l2) {
        ListNode dummy = ListNode(0);
        ListNode* tail = &dummy;
        while (l1 && l2) {
            if (l1->val > l2->val) swap(l1, l2);
            tail->next = l1;
            tail = tail->next;
            l1 = l1->next;
        }
        tail->next = l1 ? l1 : l2;
        return dummy.next;
    }
};

先不斷的一分為二，再兩兩合併。
slow指標每次走一步，fast指標每次走二步，可用此法找出中間點。
合併時，不斷找兩list中最小值，當作下一個節點。

Bottom-Up link-list merge sort.

Time complexity : O(n log(n))
Space complexity : O(1)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (!head) return nullptr;
        
        int len = 0;
        for (ListNode* cur=head; cur!=nullptr; cur=cur->next)
            ++len;
        
        ListNode dummy(0);
        dummy.next = head;
        ListNode* tail;
        ListNode *l, *r, *rest;
        for (int n=1; n<len; n<<=1) {
            rest = dummy.next;
            tail = &dummy;
            while (rest) {
                l = rest;
                r = split(l, n);
                rest = split(r, n);
                auto merged = merge(l, r);
                tail->next = merged.first;
                tail = merged.second;
            }
        }
        return dummy.next;
    }
private:
    ListNode* split(ListNode* head, int n) {
        while (head && --n) 
            head = head->next;
        ListNode *next_start = head ? head->next : nullptr;
        if (head) head->next = nullptr;
        return next_start;
    }
    
    pair<ListNode*, ListNode*> merge(ListNode* l, ListNode* r) {
        ListNode dummy(0);
        ListNode* tail = &dummy;
        while (l && r) {
            if (l->val > r->val) swap(l, r);
            tail->next = l;
            tail = tail->next;
            l = l->next;
        }
        if (l) tail->next = l;
        if (r) tail->next = r;
        while (tail->next) tail = tail->next;
        return {dummy.next, tail};
    }
};

相較於Top-Down，Bottom-Up沒有不斷的從中點切，而是直接將原list視為已切分好的list，2個一組、4個一組、8個一組、…往上合併。
無需遞迴、而且操作上是in-place。