Given a node in a binary search tree, find the in-order successor of that node in the BST.

If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node:

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

Follow up:

Could you solve it without looking up any of the node’s values?

Example 1:

Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.

Example 2:

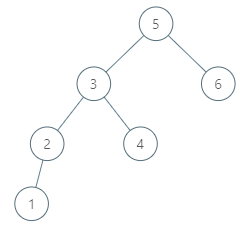
Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
Output: 17

Example 4:

Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13
Output: 15

Example 5:

Input: tree = [0], node = 0
Output: null

Constraints:

-10^5 <= Node.val <= 10^5
1 <= Number of Nodes <= 10^4
All Nodes will have unique values.

Solution

Time complexity : O(h)
Space complexity : O(1)

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* inorderSuccessor(Node* node) {
        if (node->right) {
            node = node->right;
            while (node->left) node = node->left;
            return node;
        }
        
        while (node->parent && node==node->parent->right)
            node = node->parent;
        
        return node->parent;
    }
};

中序：左中右。

中序巡訪的下一個(successor)為：

若有右子樹，則為右子樹的最小者。
若無右子樹，以現在的node來說，中序結束了，要回去了，又以目標node(左中右)來說，目前是在它的「左」，要往上巡訪到node為left child，回傳其parent。