[LeetCode August Challange]Day30-Largest Component Size by Common Factor
Given a non-empty array of unique positive integers A, consider the following graph:
- There are A.length nodes, labelled A[0] to A[A.length - 1];
- There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1. Return the size of the largest connected component in the graph.
Example 1:

Input: [4,6,15,35]
Output: 4
Example 2:

Input: [20,50,9,63]
Output: 2
Example 3:
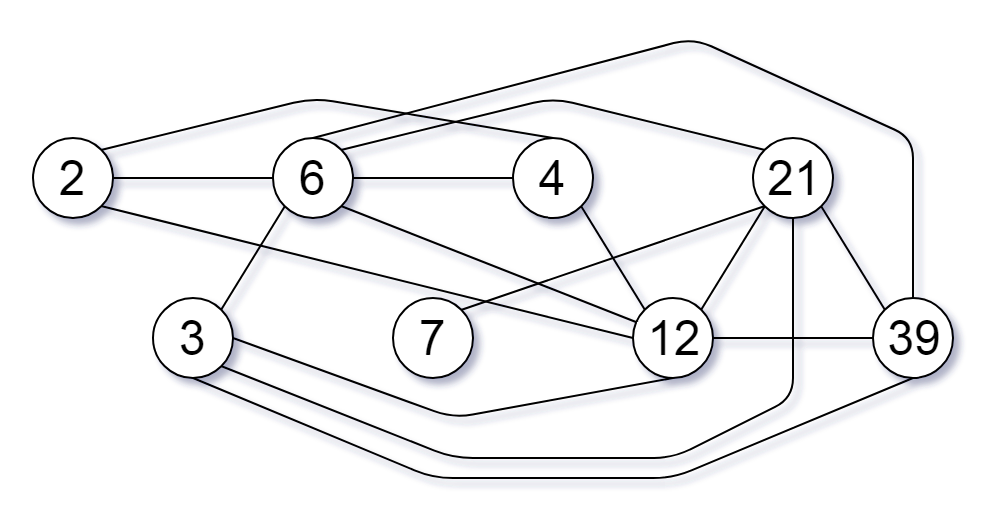
Input: [2,3,6,7,4,12,21,39]
Output: 8
Note:
- 1 <= A.length <= 20000
- 1 <= A[i] <= 100000
Solution
Time complexity : O(sum(sqrt(A[i])))
Space complexity : O(max(A))
class Solution {
public:
int largestComponentSize(vector<int>& A) {
int max_num = *max_element(A.begin(), A.end());
DSU dsu(max_num+1);
for (int num: A) {
for (int i=2; i<=sqrt(num); ++i) {
if (num%i == 0) {
dsu.Union(num, i);
dsu.Union(num, num/i);
}
}
}
unordered_map<int, int> parent_cnt;
int ans = 1;
for (int num: A) {
ans = max(ans, ++parent_cnt[dsu.find(num)]);
}
return ans;
}
private:
struct DSU {
vector<int> parent_;
DSU(int n) {
parent_ = vector<int>(n);
for(int i=0; i<n; ++i)
parent_[i] = i;
}
int find(int x) {
if (parent_[x] != x)
parent_[x] = find(parent_[x]);
return parent_[x];
}
void Union(int x, int y) {
parent_[find(x)] = parent_[find(y)];
}
};
};
使用並查集資料結構。
以 [4, 6, 15, 35] 為例,圖解一下操作。
一開始初始化,各num的parent都為自己。 (其實有0~35,忽略沒用到的)
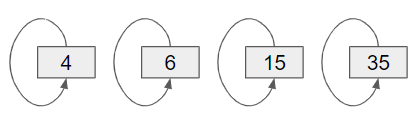
開始union。
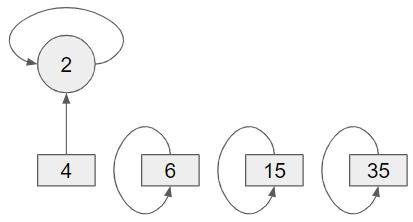


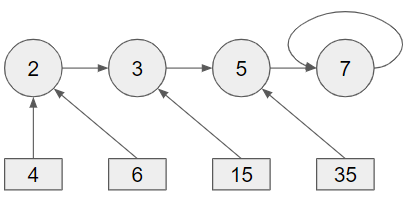
最後對輸入陣列中所有數字進行find,會找到它的最根源,而這四個數字的最根源都是7,故7會被計數4次。