Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

Input: [1,2,3,0,2]
Output: 3 
Explanation: transactions = [buy, sell, cooldown, buy, sell]

solution

time complexity : O(n)
space complexity : O(1)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int hold = INT_MIN, sold = 0, rest = 0;
        
        for (int price: prices) {
            int preSold = sold;
            sold = hold + price;
            hold = max(hold, rest-price);
            rest = max(rest, preSold);
        }
        
        return max(rest, sold);
    }
};

若是用暴力法，可將一系列當天做的事，視為一3進位字串，例：

[1,2,3,0,2]
"b s r b  s" (2-1)+(2-0)=3

一一列舉合法字串，再計算出相對應的獲利，從中找出最大值，O(3^n)。

動態規劃的方法：題目的rest、buy、sell狀態之間的轉換，可用下圖表示：

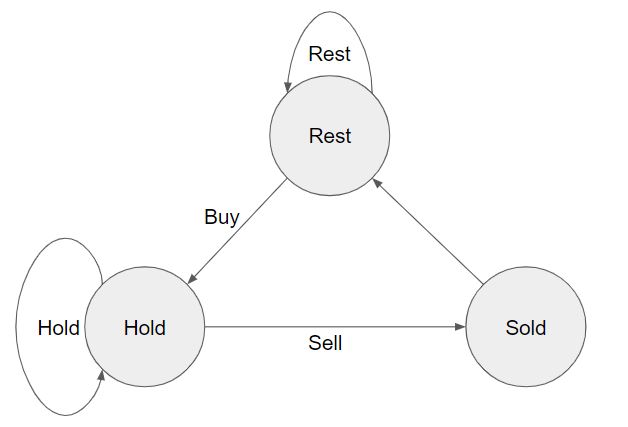
代表目前第i個時間點，所能獲得的最高利益。

目前閒置或rest狀態最大獲益，是由上一個時間點rest或是sold兩者之間的最大值。
rest[i] = max(rest[i-1], sold[i-1])
目前持有股票的狀態最大獲益，是由上一個時間點的rest買入(-price)，與上一個時間點還持有(hold)股票之間的最大值。
hold[i] = max(hold[i-1], rest[i]-price)
目前售出股票的狀態最大獲益，等於上一個時間點持有(hold)的最大獲益加上此時的price。
sold = hold[i-1]+price

最後的最大收益，是sold與rest取最大者，不考慮hold的原因是，都最後一天了，持有或不賣出甚至買入，對最後的收益都是負影響的。